『图论』入门以及 Hierholzer 算法 |
您所在的位置：网站首页 › varies in its favor › 『图论』入门以及 Hierholzer 算法 |
『图论』入门以及 Hierholzer 算法
|
写在前面 最近在 LeetCode 上随机刷题，打算复习以前学过的算法，同时学一点新算法。正巧这两天做到图论相关的题目，就顺手记一下这个算法——用于求解欧拉路径的 Hierholzer 算法。 为了便于理解，本文中的一些叙述可能不太严谨，敬请理解。 图论基础知识图( \mathbf{Graph} )：简单地说构成一张图的要素有两个——顶点和边。顶点之间用边连起来，就构成了一张图。另外，类比子集的概念，还存在着子图的概念。有向图：也就是说，图中的边都是有方向的，即单向。有向边限制了路径，就如同下面的图中，从1到2可以 1\Longrightarrow2 ，但是要从2到1就必须 2\Longrightarrow4\Longrightarrow1 。例子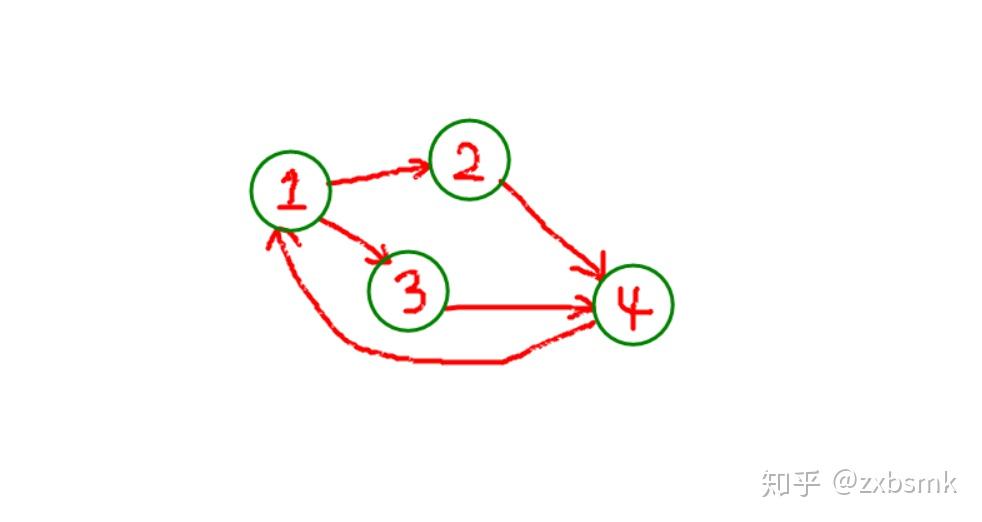： 含有4个顶点和5条边的有向图无向图：也就是图中的边是没有方向的，也就是说可以双向通行。如果上图中的边都是无向边，那么就可以 2\Longrightarrow1 。度：这是与顶点相关的概念，通常会说一个点的度数是多少。若顶点记为 V ，其度数可记为 \deg(D) 。无向图中，顶点的度数就是和这个顶点相连的边数。有向图中，度又可以分为入度和出度，入度指的是指向当前顶点的边数，出度指的是从当前顶点出发的边数，度数就等于入度加出度。如上图中，顶点1的入度为1、出度为2。欧拉路径：如果在一张图中，可以从一点出发遍历所有的边，那么遍历过程中的这条路径就叫做欧拉路径。如果这条路径是闭合的，那就称为欧拉回路。简单地说，如果一张图可以被“一笔画”，那么“一笔画”的那个轨迹就叫做欧拉路径。欧拉图判定定理：含有欧拉回路的图称为欧拉图，含有欧拉路径的图称为半欧拉图。无向图中，如果所有顶点的度数都为偶数，则为欧拉图；如果有两个顶点的度数为奇数，其他的为偶数，则为半欧拉图。有向图中，如果所有顶点的入度等于出度，那么就是欧拉图。判定半欧拉图的方法也很简单，大家可以自行推理。其他相关知识栈：这是一个计算机术语，是一个抽象的概念，人为造出来的。简单的理解就是一个桶，向里面放东西，一开始放进去的东西在最底下，后面的叠在上面。所以如果要把最开始放的东西拿出来，就必须把上面的东西都拿走。对于栈而言，显然是“后来者居上”，遵循着“先进后出”的规则。平时我们说到栈，指的是那个放东西的桶，以及这种放东西的方法。队列：其实本文与队列无关，但是都说到栈了，也就顺口提一下与栈相对的队列。既然有“后来者居上”，自然也有“先到先得”。队列就像是日常生活中的排队一样，遵循“先进先出”的规则。Hierholzer 算法问题简述：现给出一个有向图，且为欧拉图。求欧拉回路。 Hierholzer 算法过程： 选择任一顶点为起点，遍历所有相邻边。深度搜索，访问相邻顶点。将经过的边都删除。如果当前顶点没有相邻边，则将顶点入栈。栈中的顶点倒序输出，就是从起点出发的欧拉回路。为了证明该算法的有效性，下说明两条性质。 性质一： 如果该图为欧拉图，则栈底的必定为起点。如果该图为半欧拉图，则栈底部存储的是与起点不同的另外一个奇度数顶点。 证明： 当顶点入栈时，说明当前所在顶点没有相邻边。 考虑到从起点出发到当前结点的路径中，除了起点和当前顶点外，其他的顶点都失去了偶数度数(入度与出度一一对应)。 如果起点和当前顶点不同，那么两者都失去了奇数度数。 如果图中包含欧拉回路，意味着所有顶点的初始度数都是偶数，而当前顶点的当前度数为0，表示当前顶点的初始度数必定是奇数，产生矛盾，因此假设不成立。当前顶点就是起点。 同样地，对于欧拉路径，当前顶点不可能是起点，否则起点的度数就是偶数，而欧拉路径中起点和终点的度数一定是奇数。因此，当前顶点不是起点，但是度数也是奇数，所以一定是终点。 性质二： 如果该图为欧拉图(/半欧拉图)，则栈中的自底到顶第 n 个顶点就是欧拉回路(/欧拉路径)上的第 n 个顶点。 证明： 在此只证明栈中相邻顶点在图中也为相邻顶点。因为模拟 Hierholzer 算法过程，可知该算法实际上就是在模拟“一笔画”过程，并且沿着画完的轨迹，从终点倒着逐一添加顶点到栈中。 并且主要以 n=2 的情况为例，后面的情况可以此类推。并且为了不用纠结于区分欧拉回路和欧拉路径，不妨以半欧拉图为例。 假设图中存在相邻的两顶点 V_1,V_2 ，并且深度搜索过程中，先访问 V_2 随后访问了 V_1 ，并且 V_1 成为第一个入栈的顶点。由性质一可知， V_1 就是欧拉路径上的起点(两个奇度数顶点任一可看作起点)。 根据 Hierholzer 算法，在遍历过程中，删除了途径的边，所以此时所有顶点的度数都为偶数。当然 \deg(V_2) 也是偶数，接下来就分类讨论。 如果 \deg(V_2)=0 ，也就是说当前顶点 V_2 成为第二个入栈的顶点，那么 n=2 的情况就证毕了。 如果 \deg(V_2)>0 ，那么考虑当前包含 V_2 的子图 \mathbf{G} ，显然 \mathbf{G} 是一个欧拉图，那么当前以 V_2 为起点继续实施 Hierholzer 算法遍历剩下的相邻边，根据性质一， V_2 将会是 \mathbf{G} 中第一个入栈的顶点。也就是， V_2 是原图中第二个入栈的顶点。 综上所述，以此类推， V_{n-1} 入栈前最后接触过的 V_n 将会是第 n 个入栈的顶点，再结合直观理解， V_n 就是路径上的第 n 个顶点。 写在后面LeetCode 上面有一道与 Hierholzer 算法配套的题目——753.破解保险箱。 有兴趣的同学可以去试试，感觉构建那个图还是挺有难度的。 其实在算法性质二的说明上不太满意，但是在网上翻了一下，又没找到关于这个算法的完整证明过程，所以就自己脑补了上面两个性质的证明，也不严谨，但能力有限只能如此了。 如果有同学有该算法原理证明的相关资料，欢迎在评论区分享。 《算法导论》上似乎有这个算法的详细说明，可惜我还没买。 且看吧。 |
【本文地址】
今日新闻 |
推荐新闻 |